Défi 13, ou la leçon de géométrie

13 décembre 2010

J'avais bien pensé à un chemisier répondant aux règles strictes des paraboloïdes elliptiques, mais j'ai crains que finalement le célèbre :

$\left( \frac{x}{a} \right) ^2 + \left( \frac{y}{b} \right) ^2 - z = 0$

ne soit pas à mon avantage !

Mon intérêt s'est alors porté sur une jupe hyperboloïde... mais là encore, j'ai douté de mes fesses coincées par un douteux

${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2}-1=0$

... allais je renoncer à ce Défi 13 ? jeter aux oubliettes mes ~~très~~ anciennes connaissances mathématiques (heu...vive Wikipedia hein ;) !) ?

croutch, croutch...

voilà qui me parlait...

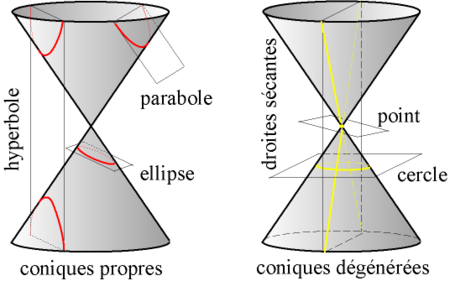
ou plus exactement le cône de révolution :

avec r = 3cm, h = 10 cm et les formules du volume V et de l'aire A (aire de la surface enfermant le cône: aire latérale + base circulaire) sont 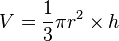$V = \frac{1}{3}\pi r^2\times h$ et $A = \pi r (r+a)\,$

où r est le rayon du cercle de base, h la hauteur du cône et $a = \sqrt{r^2 + h^2}$

l'apothème du cône. L'aire latérale A_l (sans la base) vaut $A_l = \pi r \sqrt{r^2 + h^2} = \pi r^2 \sqrt{1 + \frac{h^2}{r^2}}$

or, d'après les relations trigonométriques dans le triangle rectangle, on a $1 + \frac{h^2}{r^2} = \frac{1}{\sin ^2\alpha}$

où α est le demi-angle au sommet. Si A₀ est l'aire de la base π⋅r ², on a alors 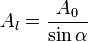$A_l = \frac{A_0}{\sin \alpha}$

Pour obtenir le patron d'un cône de révolution de rayon r et de hauteur h, il faut d'abord calculer l'apothème

$a=\sqrt{r^2+h^2}$

Il suffit alors de tracer un cercle de rayon r et une portion de cercle de rayon a dont l'angle au centre vaut $\frac{r}{a}$ de l'angle plein.

ouhou ????? vous êtes encore là ?

Edit : heu, non je ne suis pas une bête en math ! comme mentionné plus haut tout cela est issu de Wikipedia ! Je vous parait plus "normale" d'un coup, non ?

Allez pour faire simple, voilà le patron :

et tout cela pour quoi ?

Chapeau de sorcière, de lutin ? 1/2 soustif futuriste ? nonnnnnnnn !!!

Fauteuil Poire pour Poupée ? nooooooonnnnnnnnnnn

Chouettes de Noël, patron maison (disponible en taille réelle sur simple demande en attendant que je le mette en ligne !), qui vont compléter ma déco du sapin ...

EDIT PATRON : cliquer sur le Chouette_Patron, ou si vous enregistrez la photo de celui-ci (voir plus haut) sur votre PC et que vous imprimez....à priori il est en taille réelle !!! j'ai testé et cela correspond ! sinon, pas de souci je peux vous l'envoyer par email !!!

ouhou ! ouhou !

fringues_345

... elles vous plaisent ? sachez qu'il y a aussi des chouettes à gagner ici !!!! il suffit de laisser un com', tirage au sort le 24 Décembre ! comme pour mon petit jeu Déco du Sapin du 12 Décembre (ou 2 possibilités de préparer sa déco de Noël un an à l'avance !!!!)

et pour admirer les réas des autres superstitieuses, c'est là :

DEFI 13

Posté par Actamis à 07:02 - Commentaires […] - Permalien [#]

Tags: defi 13, tuto

Partager cet article

Vous aimez ?

1 vote

Traditions d'Alsace #3

Babouch, bababouch....Babouchka* !!!!!

Commentaires

Lamalleacreation

11/01/2016 14:54

et bien cette année moi les chouettes ont décoré mon sapin http://lamalleacreation.canalblog.com/

Domi

07/11/2014 07:47

merci pour cette jolie idée voici le résultat sur ma page FB https://www.facebook.com/pages/La-malle-%C3%A0-cr%C3%A9ation/1468588743423439?hc_location=timeline

Blanche Neige

08/12/2011 08:05

Merci pour le pdf!!! Je vais essayer d'en faire pour décorer ma maison en cette période de fêtes. Les tiennes sont très mignonnes, et des chouettes en liberty, c'est la classe!

Rosalie and Co

05/12/2011 08:55

GENIAL !! et tres réussi !! j'adore

Magali

15/02/2011 11:03

Très sympa ces chouettes :) Je ne sais pas si cela peut vous intéresser mais nous organisons un concours cuto couture sur la Communauté de Loisirs Créatifs de Cultura, C'MonAtelier, avec la réalisation d'une guirlande de tissus originale... Toutes les conditions sont ici :http://cmonatelier.cultura.com/space/communaute-custo-couture/content/5eme-defi-creatif-c-monatelier_9C1A9E9D-C647-44FF-90D7-9D3A70123075 A bientôt peut être :) Magali